AVL(Adelson-Velsky and Landis)TREE
AVL의 full form은 발명자의 이름이다.
먼저 AVL 트리의 특징에 대해서 살펴보자.
특징
- 이진탐색트리의 속성을 그대로 가진다.
- 왼쪽, 오른쪽 서브트리의 높이 차이가 최대 1이어야 한다.
- 높이 차이가 1보다 커지면 Rotation을 통해 균형을 맞춘다.
Rotation 방식을 설명하기 전에, 먼저 높이 차이를 비교하는 BF에 대해서 먼저 이해할 필요가 있다.
BF(Balance Factor) $ BF(K) = K_{leftHeight} - K_{rightHeight} $, K = Node
수식처럼 노드의 왼쪽 높이와 오른쪽 높이를 비교하는 요소를 BF 라고 한다. 만약 height의 의미가 이해가 안된다면, 트리의 특징에서 height가 무엇을 의미하는지 찾아보는 것이 좋을 것 같다. 이제 이어서 동작 방식을 살펴보자.
동작방식
- BF를 활용해 AVL 트리의 균형을 확인한다.
- BF에 값에 따라 좌회전 or 우회전을 한다.
위에서 보이는 좌회전, 우회전의 동작방식을 먼저 이해할 필요가 있다.
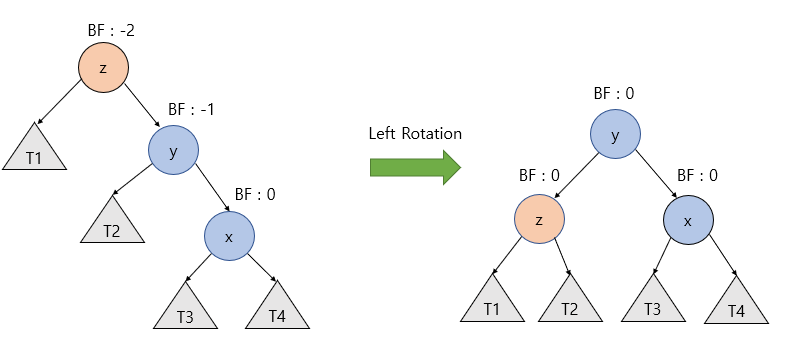
좌회전 동작방식
- y의 왼쪽 자식노드를 z 노드로 변경한다.
- 기존의 y의 왼쪽 자식노드를 z의 오른쪽 자식 노드로 변경한다.
이것만 보면 이해하기가 어려운데 간단하게 코드로 보면 이해하기가 더 쉬울 수있다.
// 좌회전
Node left_rotation(Node n) {
Node childRight = n.getRightNode();
Node grandChildLeft = childRight.getLeftNode();
childRight.setLeftNode(n);
childRight.getLeftNode().setRightNode(grandChildleft);
return childRight;
}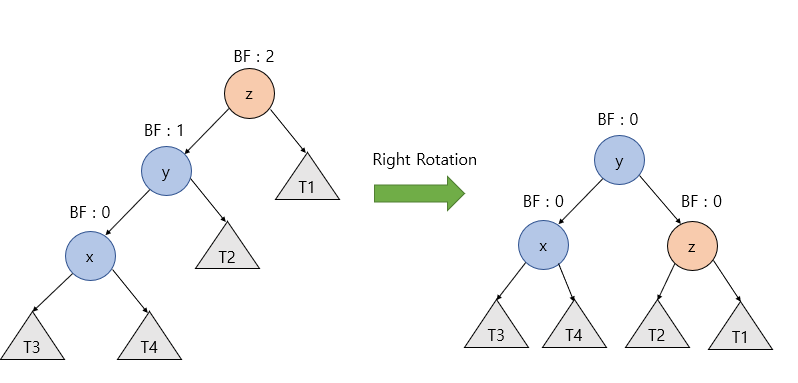
우회전 동작방식
- y의 오른쪽 자식노드를 z노드로 변경한다.
- 기존의 y의 오른쪽 자식노드를 z의 왼쪽 자식 노드로 변경한다.
이것도 코드로 한 번 살펴보자.
// 우회전
Node right_rotation(Node n) {
Node childLeft = n.getLeftNode();
Node grandChildRight = childLeft.getRightNode();
childLeft.setRightNode(n);
childLeft.getRightNode().setLeftNode(grandChildleft);
return childLeft;
}이 부분을 공부하면서 음수는 좌회전을 양수는 우회전을 하면 되지 않을까? 라는 생각을 했는데, 이어지는 AVL 트리가 무너진 케이스를 보니 꼭 그렇지는 않은 것을 알 수 있었다.
AVL 트리 무너진 경우
- LL(Left Left) CASE
- RR(Right Right) CASE
- LR(Left Right) CASE
- RL(Right Left) CASE
1번부터 차례대로 살펴보자.
LL(Left Left) CASE
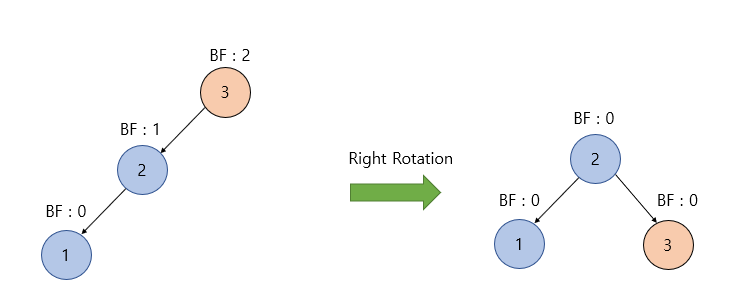
- 상황 : BF가 -1 ~ 1 범위를 벗어나고 탐색 노드 이후로 노드가 왼쪽 -> 왼쪽 으로 이어져 있는 상황
- 해결 : 우회전을 이용하여 해결 가능
RR(Right Right) CASE
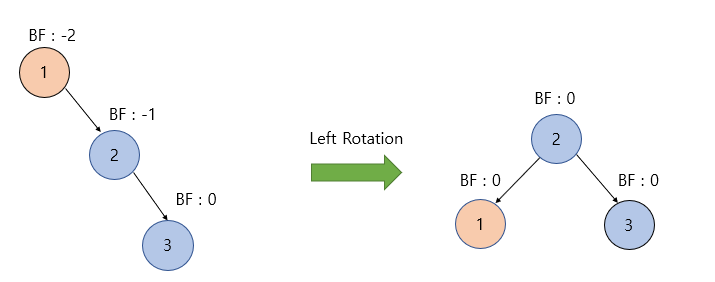
- 상황 : BF가 -1 ~ 1 범위를 벗어나고 탐색 노드 이후로 노드가 오른쪽 -> 오른쪽으로 이어져 있는 상황
- 해결 : 좌회전을 이용하여 해결 가능
LL CASE와 RR CASE는 직관적이여서 이해하기에 어렵지 않다. 이어서 LR CASE와 RL CASE는 조금 헷갈릴 수 있는데, 위에 있는 코드와 더불어서 살펴보면 이해하기에 어렵지 않을 것 이다.
LR(Left Right) CASE
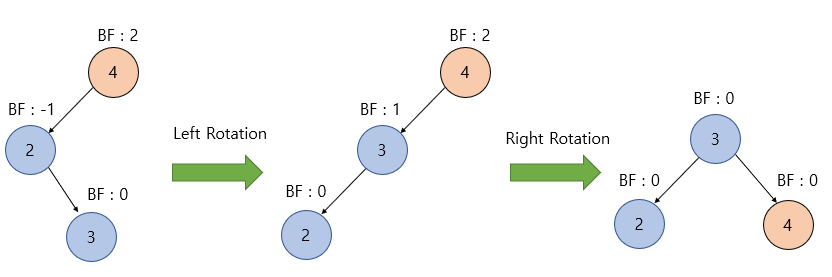
- 상황 : BF가 -1 ~ 1을 벗어나고 탐색 노드로부터 자식 노드가 왼쪽 노드 -> 오른쪽 노드로 이어진 상황
- 해결
- 먼저 탐색노드의 왼쪽 자식 노드에 대하여 좌회전을 수행한다.
- 좌회전 수행이후, LL CASE로 변하게 되고, 탐색 노드에 대하여 우회전을 수행한다.
해당 파트에서 순서대로 따라가다 보면 이해가 안 될 수 있는 부분이 있다. 이 부분에서 상당히 해맸었다.
첫번 째 해결방법에서 탐색노드의 왼쪽 자식 노드에 대하여 좌회전을 수행했다. 그림대로 순서를 따라가면 다음과 같다.
- 3번 노드의 왼쪽 자식노드로 2번 노드를 연결한다.
- 3번 노드의 원래 있던 왼쪽 자식노드를 2번 노드의 오른쪽 자식노드로 연결해야 하는데, 없으므로 비운다.
- 4번 노드는 아직 2번 노드를 가리키고 있는데..? 그림이 이상한데? 3번노드는?
이라는 상황에 직면하게 되는데, LR CASE의 코드 수행시 다음과 같이 수행하기 때문에 변하게 된 노드에 대하여 탐색 노드의 연결을 유지할 수 있다.
Node searchNode; // 탐색노드라고 가정
// LR CASE 발견!
// searchNode.setLeftNode(left_rotatation(searchNode.getLeftNode());
Node changedNode = left_rotatation(searchNode.getLeftNode());
searchNode.setLeftNode(changedNode);
// LL 수행이 부분을 이해하는데에 사실 좀 많은 시간이 걸렸다. 회전 시 반환 값으로 회전 된 서브트리의 루트노드를 반환한다.
따라서 이 반환된 노드를 다시 탐색한 노드의 왼쪽 자식 노드로 설정하기 때문에, 해당 모양의 트리가 완성되는 것이다.
이 부분을 꼭 이해해야한다. 이 부분을 이해하면 RL CASE는 어렵지 않게 이해할 수 있다.
RL(Right Left) CASE
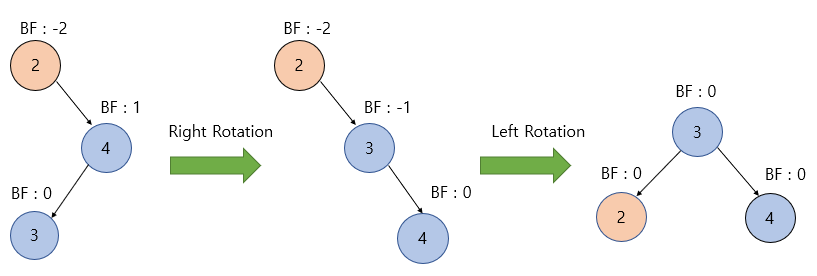
- 상황 : BF가 -1 ~ 1을 벗어나고 탐색 노드로부터 자식 노드가 오른쪽 노드 -> 왼쪽 노드로 이어진 상황
- 해결
- 먼저 탐색노드의 오른쪽 자식 노드에 대하여 우회전을 수행한다.
- 우회전 수행이후, RR CASE로 변하게 되고, 탐색 노드에 대하여 좌회전을 수행한다.
위에 LR CASE를 이해하고 나면 RL CASE는 이해하기 쉬울 것이다.
남겨진 노드에 대해 어떻게 연결되는지 이해하는지가 관건이었던 것 같다.
참고 : https://code-lab1.tistory.com/61
'Computer Science > Data Structure' 카테고리의 다른 글
| 편향 이진탐색트리를 해결하기 위한 방법(2) RED-BLACK TREE (0) | 2023.04.13 |
|---|---|
| Hash Fuction, Hash Table, Hash Collision (0) | 2023.04.11 |
AVL(Adelson-Velsky and Landis)TREE
AVL의 full form은 발명자의 이름이다.
먼저 AVL 트리의 특징에 대해서 살펴보자.
특징
- 이진탐색트리의 속성을 그대로 가진다.
- 왼쪽, 오른쪽 서브트리의 높이 차이가 최대 1이어야 한다.
- 높이 차이가 1보다 커지면 Rotation을 통해 균형을 맞춘다.
Rotation 방식을 설명하기 전에, 먼저 높이 차이를 비교하는 BF에 대해서 먼저 이해할 필요가 있다.
BF(Balance Factor) , K = Node
수식처럼 노드의 왼쪽 높이와 오른쪽 높이를 비교하는 요소를 BF 라고 한다. 만약 height의 의미가 이해가 안된다면, 트리의 특징에서 height가 무엇을 의미하는지 찾아보는 것이 좋을 것 같다. 이제 이어서 동작 방식을 살펴보자.
동작방식
- BF를 활용해 AVL 트리의 균형을 확인한다.
- BF에 값에 따라 좌회전 or 우회전을 한다.
위에서 보이는 좌회전, 우회전의 동작방식을 먼저 이해할 필요가 있다.

좌회전 동작방식
- y의 왼쪽 자식노드를 z 노드로 변경한다.
- 기존의 y의 왼쪽 자식노드를 z의 오른쪽 자식 노드로 변경한다.
이것만 보면 이해하기가 어려운데 간단하게 코드로 보면 이해하기가 더 쉬울 수있다.
// 좌회전
Node left_rotation(Node n) {
Node childRight = n.getRightNode();
Node grandChildLeft = childRight.getLeftNode();
childRight.setLeftNode(n);
childRight.getLeftNode().setRightNode(grandChildleft);
return childRight;
}
우회전 동작방식
- y의 오른쪽 자식노드를 z노드로 변경한다.
- 기존의 y의 오른쪽 자식노드를 z의 왼쪽 자식 노드로 변경한다.
이것도 코드로 한 번 살펴보자.
// 우회전
Node right_rotation(Node n) {
Node childLeft = n.getLeftNode();
Node grandChildRight = childLeft.getRightNode();
childLeft.setRightNode(n);
childLeft.getRightNode().setLeftNode(grandChildleft);
return childLeft;
}이 부분을 공부하면서 음수는 좌회전을 양수는 우회전을 하면 되지 않을까? 라는 생각을 했는데, 이어지는 AVL 트리가 무너진 케이스를 보니 꼭 그렇지는 않은 것을 알 수 있었다.
AVL 트리 무너진 경우
- LL(Left Left) CASE
- RR(Right Right) CASE
- LR(Left Right) CASE
- RL(Right Left) CASE
1번부터 차례대로 살펴보자.
LL(Left Left) CASE

- 상황 : BF가 -1 ~ 1 범위를 벗어나고 탐색 노드 이후로 노드가 왼쪽 -> 왼쪽 으로 이어져 있는 상황
- 해결 : 우회전을 이용하여 해결 가능
RR(Right Right) CASE

- 상황 : BF가 -1 ~ 1 범위를 벗어나고 탐색 노드 이후로 노드가 오른쪽 -> 오른쪽으로 이어져 있는 상황
- 해결 : 좌회전을 이용하여 해결 가능
LL CASE와 RR CASE는 직관적이여서 이해하기에 어렵지 않다. 이어서 LR CASE와 RL CASE는 조금 헷갈릴 수 있는데, 위에 있는 코드와 더불어서 살펴보면 이해하기에 어렵지 않을 것 이다.
LR(Left Right) CASE

- 상황 : BF가 -1 ~ 1을 벗어나고 탐색 노드로부터 자식 노드가 왼쪽 노드 -> 오른쪽 노드로 이어진 상황
- 해결
- 먼저 탐색노드의 왼쪽 자식 노드에 대하여 좌회전을 수행한다.
- 좌회전 수행이후, LL CASE로 변하게 되고, 탐색 노드에 대하여 우회전을 수행한다.
해당 파트에서 순서대로 따라가다 보면 이해가 안 될 수 있는 부분이 있다. 이 부분에서 상당히 해맸었다.
첫번 째 해결방법에서 탐색노드의 왼쪽 자식 노드에 대하여 좌회전을 수행했다. 그림대로 순서를 따라가면 다음과 같다.
- 3번 노드의 왼쪽 자식노드로 2번 노드를 연결한다.
- 3번 노드의 원래 있던 왼쪽 자식노드를 2번 노드의 오른쪽 자식노드로 연결해야 하는데, 없으므로 비운다.
- 4번 노드는 아직 2번 노드를 가리키고 있는데..? 그림이 이상한데? 3번노드는?
이라는 상황에 직면하게 되는데, LR CASE의 코드 수행시 다음과 같이 수행하기 때문에 변하게 된 노드에 대하여 탐색 노드의 연결을 유지할 수 있다.
Node searchNode; // 탐색노드라고 가정
// LR CASE 발견!
// searchNode.setLeftNode(left_rotatation(searchNode.getLeftNode());
Node changedNode = left_rotatation(searchNode.getLeftNode());
searchNode.setLeftNode(changedNode);
// LL 수행이 부분을 이해하는데에 사실 좀 많은 시간이 걸렸다. 회전 시 반환 값으로 회전 된 서브트리의 루트노드를 반환한다.
따라서 이 반환된 노드를 다시 탐색한 노드의 왼쪽 자식 노드로 설정하기 때문에, 해당 모양의 트리가 완성되는 것이다.
이 부분을 꼭 이해해야한다. 이 부분을 이해하면 RL CASE는 어렵지 않게 이해할 수 있다.
RL(Right Left) CASE

- 상황 : BF가 -1 ~ 1을 벗어나고 탐색 노드로부터 자식 노드가 오른쪽 노드 -> 왼쪽 노드로 이어진 상황
- 해결
- 먼저 탐색노드의 오른쪽 자식 노드에 대하여 우회전을 수행한다.
- 우회전 수행이후, RR CASE로 변하게 되고, 탐색 노드에 대하여 좌회전을 수행한다.
위에 LR CASE를 이해하고 나면 RL CASE는 이해하기 쉬울 것이다.
남겨진 노드에 대해 어떻게 연결되는지 이해하는지가 관건이었던 것 같다.
참고 : https://code-lab1.tistory.com/61
'Computer Science > Data Structure' 카테고리의 다른 글
| 편향 이진탐색트리를 해결하기 위한 방법(2) RED-BLACK TREE (0) | 2023.04.13 |
|---|---|
| Hash Fuction, Hash Table, Hash Collision (0) | 2023.04.11 |
